Limit Fungsi: Konsep Matematika yang Penting

Ilustrasi(sfu.ca)

DALAM ranah matematika, konsep limit fungsi memegang peranan krusial sebagai fondasi bagi pemahaman kalkulus dan analisis real. Limit fungsi menggambarkan perilaku suatu fungsi ketika input mendekati nilai tertentu. Pemahaman mendalam tentang limit fungsi memungkinkan kita untuk menganalisis kontinuitas, turunan, dan integral, yang merupakan pilar-pilar utama dalam matematika dan aplikasinya di berbagai bidang ilmu.

Esensi Limit Fungsi

Secara intuitif, limit fungsi menjelaskan nilai yang didekati oleh suatu fungsi ketika variabel independennya mendekati suatu nilai tertentu. Perlu ditekankan bahwa limit tidak harus sama dengan nilai fungsi pada titik tersebut. Bahkan, fungsi mungkin tidak terdefinisi pada titik tersebut, namun limitnya tetap ada. Konsep ini sangat penting dalam memahami perilaku fungsi di sekitar titik-titik singular atau titik-titik di mana fungsi tidak kontinu.

Definisi formal limit fungsi menggunakan epsilon-delta, yang memberikan definisi matematis yang presisi tentang apa artinya suatu fungsi mendekati suatu nilai tertentu. Definisi ini menyatakan bahwa untuk setiap epsilon positif (seberapa dekat kita ingin nilai fungsi dengan limit), terdapat delta positif (seberapa dekat variabel independen harus dengan titik yang didekati) sedemikian sehingga jika variabel independen berada dalam jarak delta dari titik tersebut, maka nilai fungsi akan berada dalam jarak epsilon dari limit. Definisi ini mungkin tampak rumit pada awalnya, tetapi merupakan dasar untuk membuktikan teorema-teorema tentang limit dan untuk memahami konsep limit secara mendalam.

Notasi Limit: Limit fungsi f(x) ketika x mendekati c ditulis sebagai lim (x→c) f(x) = L. Notasi ini menyatakan bahwa ketika x mendekati c, nilai f(x) mendekati L.

Aplikasi Limit Fungsi

Limit fungsi memiliki aplikasi yang luas dalam berbagai bidang matematika dan ilmu pengetahuan. Beberapa aplikasi penting meliputi:

1. Kalkulus: Limit adalah dasar dari kalkulus. Turunan dan integral didefinisikan menggunakan limit. Turunan mengukur laju perubahan suatu fungsi, sedangkan integral mengukur luas di bawah kurva.
2. Analisis Real: Limit digunakan untuk mendefinisikan kontinuitas, konvergensi deret, dan konsep-konsep penting lainnya dalam analisis real.
3. Fisika: Limit digunakan untuk mendefinisikan kecepatan sesaat, percepatan sesaat, dan konsep-konsep penting lainnya dalam fisika.
4. Ekonomi: Limit digunakan untuk menganalisis perilaku pasar, seperti elastisitas permintaan dan penawaran.
5. Teknik: Limit digunakan dalam berbagai aplikasi teknik, seperti analisis stabilitas sistem kontrol dan desain filter.

Menghitung Limit Fungsi

Terdapat berbagai teknik untuk menghitung limit fungsi, tergantung pada bentuk fungsi dan titik yang didekati. Beberapa teknik umum meliputi:

1. Substitusi Langsung: Jika fungsi kontinu pada titik yang didekati, maka limit dapat dihitung dengan mensubstitusikan nilai titik tersebut ke dalam fungsi.
2. Faktorisasi: Jika fungsi memiliki bentuk tak tentu (seperti 0/0 atau ∞/∞), maka faktorisasi dapat digunakan untuk menyederhanakan fungsi dan menghilangkan bentuk tak tentu.
3. Merasionalkan: Jika fungsi melibatkan akar kuadrat, maka merasionalkan dapat digunakan untuk menyederhanakan fungsi dan menghilangkan bentuk tak tentu.
4. Aturan L'Hôpital: Jika fungsi memiliki bentuk tak tentu 0/0 atau ∞/∞, maka aturan L'Hôpital dapat digunakan untuk menghitung limit. Aturan ini menyatakan bahwa limit dari hasil bagi dua fungsi sama dengan limit dari hasil bagi turunan fungsi-fungsi tersebut.
5. Teorema Apit (Squeeze Theorem): Jika suatu fungsi diapit oleh dua fungsi lain yang memiliki limit yang sama pada titik yang didekati, maka fungsi tersebut juga memiliki limit yang sama pada titik tersebut.

Limit Sepihak

Limit sepihak adalah limit yang dihitung hanya dari satu sisi titik yang didekati. Limit dari kiri ditulis sebagai lim (x→c-) f(x), sedangkan limit dari kanan ditulis sebagai lim (x→c+) f(x). Limit suatu fungsi ada jika dan hanya jika limit dari kiri dan limit dari kanan ada dan sama.

Limit sepihak penting dalam menganalisis fungsi-fungsi yang tidak kontinu pada suatu titik. Misalnya, fungsi tangga (step function) memiliki limit sepihak yang berbeda pada titik-titik diskontinuitasnya.

Kontinuitas Fungsi

Konsep limit sangat erat kaitannya dengan kontinuitas fungsi. Suatu fungsi dikatakan kontinu pada suatu titik jika limit fungsi pada titik tersebut ada, nilai fungsi pada titik tersebut ada, dan limit fungsi sama dengan nilai fungsi pada titik tersebut. Secara formal, fungsi f(x) kontinu di x = c jika:

1. f(c) terdefinisi.
2. lim (x→c) f(x) ada.
3. lim (x→c) f(x) = f(c).

Kontinuitas adalah sifat penting dari fungsi karena memungkinkan kita untuk menghitung limit dengan substitusi langsung dan untuk menggunakan teorema-teorema kalkulus. Fungsi-fungsi yang kontinu banyak ditemukan dalam aplikasi matematika dan ilmu pengetahuan.

Limit di Tak Hingga

Limit di tak hingga menggambarkan perilaku suatu fungsi ketika variabel independennya mendekati tak hingga (positif atau negatif). Limit di tak hingga ditulis sebagai lim (x→∞) f(x) atau lim (x→-∞) f(x). Limit ini memberikan informasi tentang perilaku asimtotik fungsi, yaitu bagaimana fungsi berperilaku ketika x menjadi sangat besar atau sangat kecil.

Untuk menghitung limit di tak hingga, kita sering membagi pembilang dan penyebut fungsi dengan pangkat tertinggi dari x. Teknik ini memungkinkan kita untuk menyederhanakan fungsi dan menentukan limitnya dengan lebih mudah.

Contoh Soal dan Pembahasan

Berikut adalah beberapa contoh soal tentang limit fungsi beserta pembahasannya:

1. Soal: Hitung lim (x→2) (x^2 + 3x - 10) / (x - 2). Pembahasan: Fungsi ini memiliki bentuk tak tentu 0/0 ketika x = 2. Kita dapat memfaktorkan pembilang menjadi (x - 2)(x + 5). Kemudian, kita dapat membatalkan faktor (x - 2) di pembilang dan penyebut. Sehingga, lim (x→2) (x^2 + 3x - 10) / (x - 2) = lim (x→2) (x + 5) = 2 + 5 = 7.
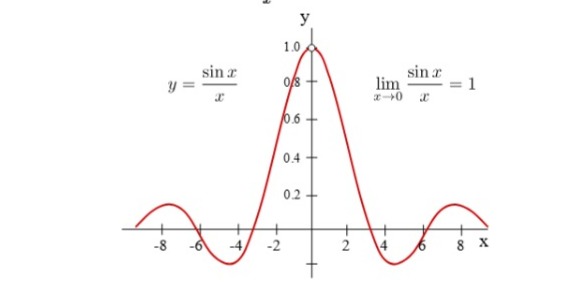
2. Soal: Hitung lim (x→0) sin(x) / x. Pembahasan: Fungsi ini memiliki bentuk tak tentu 0/0 ketika x = 0. Kita dapat menggunakan aturan L'Hôpital untuk menghitung limit. Turunan dari sin(x) adalah cos(x), dan turunan dari x adalah 1. Sehingga, lim (x→0) sin(x) / x = lim (x→0) cos(x) / 1 = cos(0) / 1 = 1.
3. Soal: Hitung lim (x→∞) (2x^2 + 5x - 3) / (3x^2 - 7x + 1). Pembahasan: Kita dapat membagi pembilang dan penyebut dengan x^2. Sehingga, lim (x→∞) (2x^2 + 5x - 3) / (3x^2 - 7x + 1) = lim (x→∞) (2 + 5/x - 3/x^2) / (3 - 7/x + 1/x^2). Ketika x mendekati tak hingga, 5/x, 3/x^2, 7/x, dan 1/x^2 mendekati 0. Sehingga, lim (x→∞) (2x^2 + 5x - 3) / (3x^2 - 7x + 1) = (2 + 0 - 0) / (3 - 0 + 0) = 2/3.

Kesalahan Umum dalam Menghitung Limit

Berikut adalah beberapa kesalahan umum yang sering dilakukan dalam menghitung limit:

1. Substitusi Langsung Tanpa Memeriksa Kontinuitas: Substitusi langsung hanya valid jika fungsi kontinu pada titik yang didekati. Jika fungsi tidak kontinu, maka substitusi langsung dapat menghasilkan jawaban yang salah.
2. Mengabaikan Bentuk Tak Tentu: Jika fungsi memiliki bentuk tak tentu, maka kita tidak dapat langsung menentukan limitnya. Kita perlu menggunakan teknik lain, seperti faktorisasi, merasionalkan, atau aturan L'Hôpital.
3. Salah Menerapkan Aturan L'Hôpital: Aturan L'Hôpital hanya dapat diterapkan jika fungsi memiliki bentuk tak tentu 0/0 atau ∞/∞. Selain itu, kita harus memastikan bahwa turunan dari pembilang dan penyebut ada.
4. Tidak Memperhatikan Limit Sepihak: Jika fungsi tidak kontinu pada suatu titik, maka kita perlu mempertimbangkan limit sepihak untuk menentukan apakah limit fungsi ada.

Teorema-Teorema Limit

Terdapat beberapa teorema penting tentang limit yang dapat membantu kita dalam menghitung limit dan memahami sifat-sifat limit. Beberapa teorema tersebut meliputi:

• Teorema Limit Jumlah: lim (x→c) [f(x) + g(x)] = lim (x→c) f(x) + lim (x→c) g(x).
• Teorema Limit Selisih: lim (x→c) [f(x) - g(x)] = lim (x→c) f(x) - lim (x→c) g(x).
• Teorema Limit Hasil Kali: lim (x→c) [f(x) g(x)] = lim (x→c) f(x) lim (x→c) g(x).
• Teorema Limit Hasil Bagi: lim (x→c) [f(x) / g(x)] = lim (x→c) f(x) / lim (x→c) g(x), asalkan lim (x→c) g(x) ≠ 0.
• Teorema Limit Pangkat: lim (x→c) [f(x)]^n = [lim (x→c) f(x)]^n.
• Teorema Limit Akar: lim (x→c) √[f(x)] = √[lim (x→c) f(x)], asalkan lim (x→c) f(x) > 0.
• Teorema Apit (Squeeze Theorem): Jika g(x) ≤ f(x) ≤ h(x) untuk semua x di dekat c (kecuali mungkin di c) dan lim (x→c) g(x) = lim (x→c) h(x) = L, maka lim (x→c) f(x) = L.

Limit Fungsi Trigonometri

Limit fungsi trigonometri sering muncul dalam kalkulus dan analisis real. Beberapa limit fungsi trigonometri yang penting meliputi:

• lim (x→0) sin(x) / x = 1.
• lim (x→0) (1 - cos(x)) / x = 0.
• lim (x→0) tan(x) / x = 1.

Limit-limit ini dapat digunakan untuk menghitung limit fungsi trigonometri yang lebih kompleks.

Limit Fungsi Eksponensial dan Logaritma

Limit fungsi eksponensial dan logaritma juga penting dalam kalkulus dan analisis real. Beberapa limit fungsi eksponensial dan logaritma yang penting meliputi:

• lim (x→0) (e^x - 1) / x = 1.
• lim (x→0) ln(1 + x) / x = 1.
• lim (x→∞) (1 + 1/x)^x = e.

Limit-limit ini dapat digunakan untuk menghitung limit fungsi eksponensial dan logaritma yang lebih kompleks.

Kesimpulan

Limit fungsi adalah konsep fundamental dalam matematika yang memiliki aplikasi luas dalam berbagai bidang ilmu. Pemahaman mendalam tentang limit fungsi memungkinkan kita untuk menganalisis kontinuitas, turunan, dan integral, serta untuk memecahkan masalah-masalah kompleks dalam matematika dan ilmu pengetahuan. Dengan menguasai teknik-teknik perhitungan limit dan memahami teorema-teorema limit, kita dapat mengembangkan kemampuan analitis dan pemecahan masalah yang kuat.

Semoga artikel ini memberikan pemahaman yang komprehensif tentang limit fungsi dan aplikasinya.

Konsep Deskripsi Contoh

Limit Fungsi	Nilai yang didekati oleh suatu fungsi ketika input mendekati nilai tertentu.	lim (x→2) x^2 = 4
Kontinuitas	Suatu fungsi kontinu jika limitnya sama dengan nilai fungsi pada titik tersebut.	f(x) = x^2 kontinu di x = 2
Limit Sepihak	Limit yang dihitung hanya dari satu sisi titik yang didekati.	lim (x→0+) √x = 0
Aturan L'Hôpital	Digunakan untuk menghitung limit bentuk tak tentu 0/0 atau ∞/∞.	lim (x→0) sin(x)/x = lim (x→0) cos(x)/1 = 1